بقلم الدكتور المهندس محمد ملحم*
الحتمية determinism هي خاصية قيّمة للغاية، وقد أعطت تاريخياً مكاسب كبيرة في الهندسة والعلوم.
هل الحتمية هي خاصة للنموذج وليست من العالم الفيزيائي؟
هل للنموذج الحتمي قيمة تنبؤية مفيدة في ظل الفوضى والتعقيد؟
هل النماذج الحتمية التي تصف سلوكيات العالم الفيزيائي هي نماذج مكتملة؟
فخّا تورينغ وجوديل
الحتمية هي فكرة بسيطة مخادعة أزعجت المفكرين لفترة طويلة. الحتمية في العالم الفيزيائي هي المبدأ القائل بأن كل ما يحدث هو أمر لا مفر منه، ومرتبط ببعض الحالات السابقة للكون. ناقش الفلاسفة الآثار المترتبة على هذا المبدأ ولا سيما من حيث تقويضه لمفهوم الإرادة الحرة. فإذا كان العالم حتمياً فإننا لا نتحمّل مسؤولية أفعالنا لأنها مُقدّرة مسبقاً.
الحتمية مفهوم دقيق تماماً، مثله مثل مفهوم الإرادة الحرة. يعترف (جون إيرمان) في كتابه التمهيدي عن الحتمية بالهزيمة في التعامل مع هذا المفهوم، إذ يقول: “لا يمكن تحقيق فهم حقيقي للحتميّة من دون بناء فلسفة شاملة للعلم”.
يُصر إيرمان على أن “الحتمية هي عقيدة حول طبيعة العالم”، والتغلب على الإشكال الأكثر غدراً يتم من خلال تبنّي مبدأ عالم الكمبيوتر النمساوي (هيرمان كوبيتز)، الذي أكّد أن الحتمية هي خاصية للنماذج وليست خاصية للعالم الفيزيائي. هذا الأمر يجعل من السهل تطبيق مفهوم الحتمية على الأنظمة الهندسية.
ينظر العلماء والمهندسون إلى العالم الفيزيائي من خلال النماذج الرياضية والنماذج الحاسوبية Model of Computing، ويقللون من اعتمادهم على الفلسفة. فإذا اقتصرت دراستنا على النماذج الحاسوبية، فإن النتيجة التي وصل إليها تورينغ توضح أننا لا نستطيع معرفة ما ستفعله بعض البرامج بمجرد النظر إلى الكود (فخ تورينغ). وإذا قمنا بتوسيع دراستنا لتشمل النماذج الرياضية، فإن نتيجة غوديل تُظهر أننا سنكون دائماً قادرين على بناء نماذج لا يمكننا تحديد صحتها أو خطئها (فخ غوديل).
إذا لم تكتفِ الطبيعة “لسبب ما لا يمكن تفسيره” بمجموعة صغيرة من النماذج الرياضية التي يمكن حوسبتها ووصفها بلغة برمجية ما، فإنها “أي الطبيعة” ستستمر حتماً بمفاجأتنا بأشياءَ لا يمكننا فهمها. قد يكون هذا محبطاً بالنسبة للعلماء، لكن بالنسبة للمهندسين فإن أفق الإبداع غير محدود، إذ يمكن الاستمرار في ابتكار لغات برمجية أو أطر رياضية جديدة، ولكن لعدم اكتمالها فلن تنتهي أبداً. في الحالتين كلتيهما نحن أمام عدم يقين ناتج إما عن قصور معرفتنا أو عن بعض العشوائية الجوهرية في العالم الفيزيائي أو في نماذجنا التي تصف هذا العالم.
العديد من النماذج الرياضية والبرامج الحاسوبية التي نصمّمها تكون حتمية، أي أننا نعرف الكثير عنها إذا لم تكن قد وقعت في فخي تورينغ وغوديل. يسعى معظم مبرمجي الكمبيوتر إلى تجنُّب هذه الفخاخ، فتكون النتيجة برامج مفهومة understandable وحتمية. لكن فكرة الحتمية هذه ليست فكرة بسيطة، ولا يمكننا مواجهة عدم اليقين دون مواجهة الحتمية أولاً.
الحتمية كخاصية للنماذج
يُعتبر النموذج حتمياً إذا أعطى انطلاقاً من حالته الأولية سلوكاً محدداً عند جميع المدخلات inputs، ويصبح غير حتمي عندما يعطي سلوكاً متغيراً (غير محدد). بمعنى آخر، يكون النموذج حتمياً إذا لم يتفاعل بطريقتين أو أكثر مع نفس الشروط. أنظر إلى الشكل (1) وهو عبارة عن نموذج يصف سلوك نظام ما، حيث يتنقل النظام بين عدة حالات states (S0, S1, S2) عند تغير الظروف (أي الدخل input). بناءً على ماتقدم النموذج المبين في الشكل (1) غير حتمي لأنه يُبدي أكثر من ردة فعل عند تأثير نفس الدخل a، حيث ينتقل إلى أكثر من حالة عند نفس الشروط (عند تطبيق الدخل a، ينتقل النظام من الحالة الأولية S0 إلى عدة حالات S0, S1, S2 عند نفس الشروط).
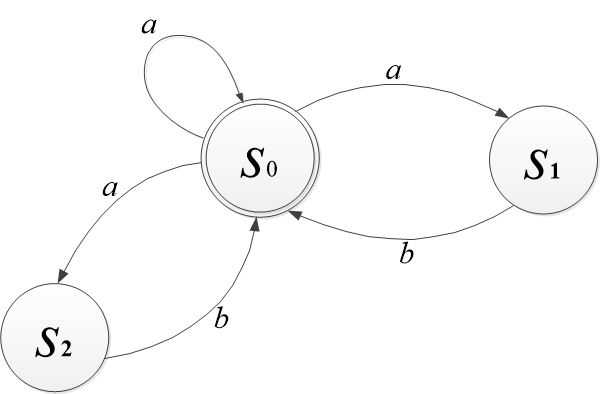
وفي مثال آخر، لتكن حالة جسم ما هي موضعه x(t) في فضاء إقليدي عند الزمنt ، حيث الزمن والموضع متحولان مستمران أي ينتميان إلى مجموعة الأعداد الحقيقية. إذا كان الدخل F(t) عبارة عن القوة المطبّقة على الجسم عند الزمن (t)، فإن سلوك الجسم في الفضاء الإقليدي بحسب قانون نيوتن الثاني هو نموذج حتمي.
يوجد نوعان من الاختلافات المفيدة لهذه الفكرة. أولاً: قد لا يحتوي النموذج على أي مدخلات وفي هذه الحالة يطلق عليه “نموذج مغلق”. على سبيل المثال، إذا افترضنا أن الكون هو كل شيء موجود، بالتالي أي نموذج للكون سيكون من دون مدخلات (لا شيء خارج الكون) فإذا تمّ إعطاء حالة ابتدائية لهذا النموذج فمن الممكن تماماً أن يكون له سلوك واحد.
ثانياً: قد يكون النموذج الحتمي قابلاً للعكس، أي يتم تحديد ماضي ومستقبل النموذج من خلال حالة النموذج عند زمن معين والمدخلات (إن وجدت) عند أي زمن. في النماذج الحتمية المغلقة القابلة للانعكاس يتحدد السلوك بأي لحظة بواسطة الحالة فقط.
أحد الأسباب التي تجعل مفهوم الحتمية مشكلة كبيرة وأمراً مُربِكاً، هو أنّ الحديث عن الحتمية يتطلّب تعريف “المدخلات Inputs” و “الحالة State” و “السلوك Behavior”، كيف يمكننا تحديد هذه الأشياء لنظام فيزيائي حقيقي؟
أي طريقة نحددها تتطلّب بناء نموذج، والتأكيد على الحتمية سيكون في الواقع تأكيداً على النموذج وليس حول الشيء الذي تمّ تصميمه. يمكن للنموذج فقط أن يكونَ حتمياً بشكل لا لُبسَ فيه.
الاستخدامات الهندسيّة والعلميّة للنماذج
يبحث المهندس عن نظام فيزيائي لمطابقة نموذجه، بينما يبحث العالم عن نموذج يُطابق نظاماً فيزيائياً. تلعب الحتمية أدواراً مختلفة في هذين الاستخدامين. تعتبر حتمية النموذج بالنسبة للمهندس مفيدة لأنها تسهّل بناء الثقة في النموذج. البوابات المنطقية (انظر الشكل (2)) كمثال على نموذج حتمي لتدفّق الإلكترونات في السيليكون. تعتبر حتمية نموذج البوابة المنطقية ذات أهمية كبيرة، فهي تعطي الثقة لمصمّمي الدارات المتكاملة لتصميم دارات تحتوي على مليارات الترانزستورات.
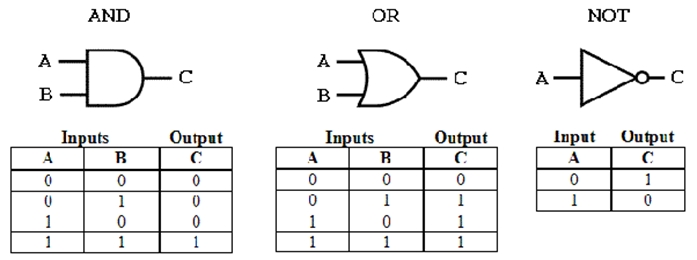
فالنموذج يتنبّأ بجميع السلوكيات حيث يمكن للمهندس تحديد كيف يتفاعل نموذج البوابة المنطقية مع أي دخل بحسب الحالة الأولية. تعتمد أهمية وفائدة نموذج البوابة المنطقية أيضاً على جودة الهيكل السيليكوني وشدّة إخلاصه للنموذج.
وهنا يكمن الاختلاف الجوهري بين العلم والهندسة. بالنسبة للعالم، لكي يكون النموذج الحتمي مفيداً يجب أن يصف سلوك النظام الفيزيائي بأمانة. بالنسبة للمهندس، لكي يكون النموذج الحتمي مفيداً يجب أن يكون من الممكن بناء نظام فيزيائي مخلصٍ لهذا النموذج. في كلتا الحالتين، تعني كلمة “مخلص faithful “: تطابق سلوكيات النموذج والنظام الفيزيائي بدرجة عالية من الدقة. على الرغم من اختلاف الأهداف إلا أنّ النماذج الحتمية ستكون مفيدة للمهندس والعالِم على حدٍّ سواء.
النماذج الهندسية الأكثر قيمة هي النماذج الحتمية. حيث لعبت حتمية هذه النماذج أهمية كبيرة في صناعة ثورة تكنولوجيا المعلومات.
بالنسبة للعالِم، عند التفكير في استخدام النماذج الحتمية، من المهم جداً أن يكون النظام الفيزيائي الذي يتمّ تصميمه حتمياًّ.
هل تدفق الإلكترونات في السيليكون حتمي؟ إذا كان المقصود هو النموذج فقط فيمكن أن يكون حتمياً بشكل لا لبس فيه. كيف يمكن الإجابة على هذا السؤال؟ الحقيقة إن جميع قوانين الفيزياء تقريباً هي نماذج حتمية، ومعظمها أيضاً قابل للعكس. قانون أوم وقانون فاراداي كلاهما نماذج حتمية قابلة للعكس. قوانين نيوتن للحركة والنظريات النسبية لأينشتاين هي حتمية أيضاً. القوانين الأساسية المستخدمة في دراسة الديناميكية الحرارية للغازات مثل قانون بويل وقانون تشارلز هي أيضاً حتمية، على الرغم من أنها لا تتطلب أن تكون الحركة الأساسية لجزيئات الغاز حتمية. حتى ميكانيك الكم هو حتمي بالكامل تقريباً من حيث تطور الدالة الموجية كما هو محدد في معادلة شرودينغر.
شيطان لا بلاس Laplace’s Demon
ظلت مسألة “ما إذا كان العالم الفيزيائي حتمياً” من دون إجابة لفترة طويلة. في أوائل القرن التاسع عشر، قدّم العالم الفرنسي بيير سيمون لابلاس حجّة للحتمية في الكون. جادل لابلاس أنه إذا كان على شخص ما (شيطان) معرفة الموقع الدقيق وسرعة كل جسيم في الكون، فسيتم تحديد موضع وسرعة كل جسيم في الماضي والمستقبل تماماً ويمكن حسابها من قوانين الميكانيك الكلاسيكية، هل هذا صحيح؟
تُعد قوانين الميكانيك الكلاسيكية مثل قانون نيوتن الثاني خاطئة ويجب تعديلها باستخدام نسبية أينشتاين لتكون دقيقة، على الرغم من أن عدم الدقة سيكون غير مهم لمعظم تطبيقات الميكانيك الكلاسيكية. علاوةً على ذلك، إن مفاهيم الموضع والسرعة التي تقف وراء فكرة “الحالة” في الميكانيك الكلاسيكي يقوّضها ميكانيك الكم، بالرغم من أنها فقط على نطاقات صغيرة للغاية. إذا كان السؤال حول ما إذا كان العالم حتمياً، فإن أي عدم دقة بغض النظر عن صغره يُعتبر مسألة يجب التوقف عندها.
هل تقوِّض الطبيعة الاحتمالية للدالة الموجية في ميكانيك الكم فكرة الكون الحتمي؟ يؤكد ستيفن هوكينغ على حتمية معادلة شرودينغر التي تصف تطور الدالة الموجية بمرور الزمن. ففي نظرية الكم، لا يحتاج المرء إلى معرفة كل من مواضع الجسيمات وسرعاتها، ويكفي أن تعرف كيف تتطوّر الدالة الموجية بمرور الزمن.
بحسب تفسير كوبنهاجن للدالة الموجية الاحتمالية الذي اقترحه الفيزيائيان الدنماركي نيلز بور والألماني فيرنر هايزنبرغ في الفترة 1925-1927، يستمر تعريف حالة النظام بالاحتمالات حتى يلاحظ المراقب الخارجي الحالة، وعند هذه النقطة فقط تؤثر الاحتمالات على النتيجة. وقبل أن تتم ملاحظتها، تبقى جميع النتائج المحتملة التي تمثّلها الاحتمالات ممكنة. وهذا يتطلب “مراقباً” منفصلاً بطريقة ما عن النظام ويقيس موضع الجسيم. التفسير المعتاد للاحتمال هو تحديد احتمالية ملاحظة نتيجة معينة للتجربة. بموجب هذا التفسير، يكون الاحتمال منطقياً فقط إذا تمّ إجراء التجربة ولاحظت النتيجة.
أدّت هذه الصعوبات إلى نقاش لا نهاية له حول معنى الدالة الموجية، مع ظهور مجموعة من المواقف التي تفترض أنّ المراقب يعيش بطريقة ما خارج الفيزياء، وأن هذا المراقب هو جوهر الإدراك البشري. ففي خمسينيات القرن الماضي استغنى الفيزيائي هيو إيفريت عن المراقب، وقام بتضمينه تحت دالة موجية واحدة تتطوّر بشكل حتمي بموجب معادلة شرودينغر.
جانب من هذه النقاشات هي فلسفية أكثر من كونها علمية، لكنه إلى حد كبير غير ذي صلة بالاستخدام الهندسي للنماذج.
لا تعتمد قيمة نموذج البوابة المنطقية الحتمي على الإطلاق على ما إذا كان انصهار الإلكترونات في السيليكون أمراً حتمياً. نحن لا نحتاج ولا نستطيع تحقيق الكمال كما يقول بوكس ودريبر، كل النماذج خاطئة ولكن بعضها مفيد، حيث أثبتت البوابات المنطقية أنها مفيدة للغاية. على الرغم من أن الحتمية يمكن أن تساعد في التنبُّؤ بكيفية تطور النظام بمرور الزمن، إلا أنه حتى النموذج الحتمي قد لا يتنبأ بالسلوك المستقبلي بشكل جيد. قد يتم إحباطه بظاهرة تسمى الفوضى والتعقيد، حيث يصبح من غير العملي حساب التنبؤات؛ أو حتى ببساطة عن طريق تراكم الأخطاء. في مثل هذه الحالات، قد تصبح النماذج غير الحتمية ذات قيمة.
يمكن إحباط النماذج الحتمية بسبب التعقيد. مثال كلاسيكي من الديناميك الحراري وهو الضغط الذي يظهره الغاز في حجرة. يمكن نمذجته على أنه تصادم الجزيئات الفردية مع بعضها البعض ومع جدران الحجرة. في أيام لابلاس، كانت هذه الاصطدامات تحكمها قوانين نيوتن الحتمية للحركة، لكن مثل هذه النماذج مستعصية على الحل. أي محاولة لحساب الحركات الفردية حتى لعدد صغير نسبياً من الجزيئات بموجب قوانين الحركة هذه سوف تستعصي حتى على أقوى أجهزة الحاسب اليوم. نتيجة لذلك، يعتبر الفيزيائيون أن هذه الحركاتِ غيرُ حتميةٍ ويعتمدون على إحصائيات أعداد كبيرة من الأحداث العشوائية لعرض السلوكيات التي تم صياغتها بشكل جيد من خلال قوانين بويل وتشارلز.
يمكن أن تنشأ السلوكيات المعقدة (الفوضى) حتى من النماذج البسيطة. إن عدم القدرة على التنبؤ بالنماذج الفوضوية بالرغم من حتميتها يمكن أن تكون خاصية مهمة وذات قيمة. تعتمد تقنية التشفير على الحتمية (لضمان إمكانية فك تشفير الرسالة من قبل المُستلم المقصود) وعلى عدم القدرة على التنبؤ (لحماية الرسالة من التنصت). على الرغم من أن مصممي التشفير اليوم يعتمدون على نماذج حتمية، فإنهم يأملون أن يكون العالم الفيزيائي في الواقع غير حتمي ويمكن استغلال شكل من أشكال “العشوائية الحقيقية” لصنع تقنيات تشفير أقوى، علماً أنّ تحقيق العشوائية الحقيقية أمر صعب للغاية.
أثر الفراشة
عمل إدوارد نورتون لورينز Edward Norton Lorenz كباحث في مجال الأرصاد الجوية في معهد ماساتشوستس للتكنولوجيا في أوائل الستينيات، واهتم بدراسة التأثيرات الجوية بهدف التنبؤ بالطقس بشكل أفضل، وتوصّل إلى نتيجة محبطة مفادها “على الرغم من حتميّة النماذج المعتمدة فإنّ التنبّؤ بالطقس بعد عدة أيام لم يكن ممكناً”. يعد لورينز من بين أول من استخدم نماذج رياضية متطورة للحمل الحراري والتأثيرات الحرارية في السوائل لبناء محاكاة حاسوبية للطقس. ومع ذلك، فقد لاحظ أن نماذجه ستسفر عن سلوكيات مختلفة جذرياً إذا بدأ المحاكاة بحالات أولية مختلفة تماماً.
إن التغير في بعض المقادير أو البارومترات غير المحسوسة سيؤدي إلى مسارين مختلفين في تطور الحالة في النموذج، وإذا كان هناك أي خطأ مهما كان صغيراً في مراقبة الحالة الحالية في النموذج أو في أي نظام حقيقي فسيصبح التنبؤ المقبول بالحالة في المستقبل مستحيلًا.
أُطلق فيما بعد على هذه الحساسية الشديدة للشروط الأولية اسم “أثر الفراشة” بعد استعارة وردت في عنوان حديث لورينز، حيث يمكن أن يتسبب الاضطراب الذي أحدثه جناح الفراشة في إعصار. حيث قام جناح الفراشة بتغيير الشروط الأولية بما يكفي فقط لإحداث فرق بين تشكل الإعصار وعدم تشكل الإعصار، أي لم يكن الإعصار ليتشكل لو لم تحلق الفراشة.
منذ وقت تجارب لورينز الأولية، تحسنت أجهزة الكمبيوتر والنماذج الرياضية والبيانات التي تم جمعها حول الطقس، ومع ذلك لا يمكن الاعتماد على التنبؤات التي تتجاوز 14 يوماً لأنماط الطقس مثل المطر والرياح. يمكن أن تؤدي الشروط الأولية التي لا يمكن تمييزها إلى طقس مختلف جذرياً.
من السمات الشائعة للنماذج التي لديها حساسية شديدة للشروط الأولية أن سلوكها يمكن أن يظهر عشوائياً ومتقلباً، وتسمى هذه الظاهرة “بالفوضى” على الرغم من حتمية النماذج. حتى النماذج البسيطة يمكن أن تظهر حساسية شديدة للشروط الأولية. يوضح الشكل (3) مسار كرة البلياردو على طاولة مع وجود عائق دائري ثابت في المنتصف. في هذه الحالة، يؤدي اختلاف بسيط في زاوية المسار الأولي للكرة إلى مسارات مختلف تماماً حول الطاولة. على الرغم من أن مسار بداية الكرة على اليسار يختلف تقريباً بشكل غير محسوس بين الخط الصلب والخط المنقّط، وينتج عنه مسار مختلف جذرياً.
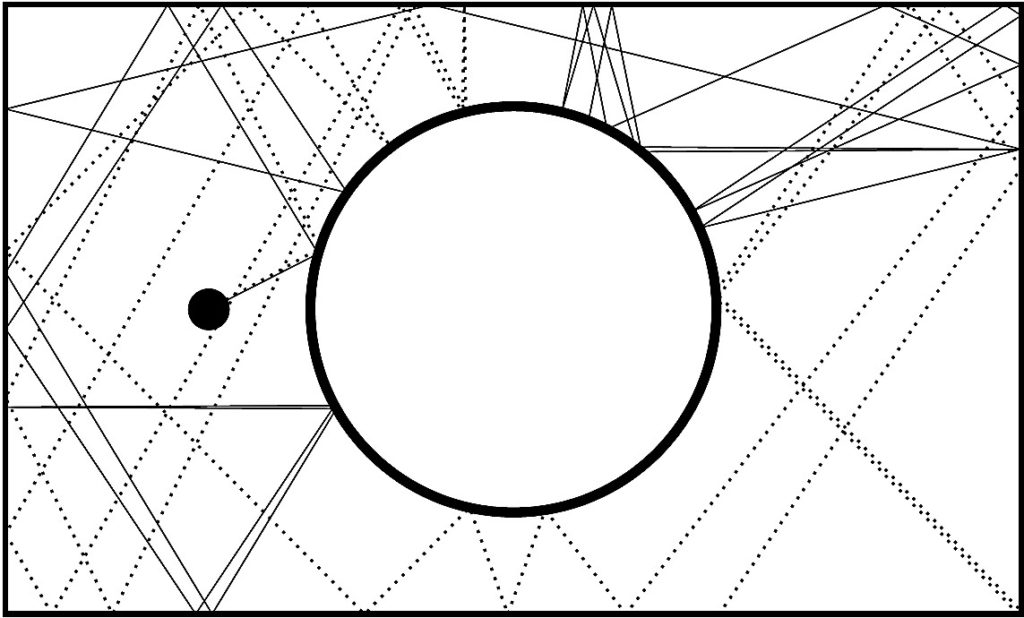
الحتمية غير المكتملة
يعتقد لابلاس أن الطبيعة يمكن وصفها بالكامل بوساطة نماذج حتمية متحولاتها مستمرة، ويذهب (ولفرام Wolfram )
إلى أبعد من ذلك ويجادل بأن الطبيعة تتصرف مثل النماذج الحاسوبية التي هي أيضاً حتمية ولكن متحولاتها متقطعة.
في عالم لابلاس، يعتبر الزمان t والمكان x متحولين مستمرين (x,t∈R ). وفي عالم ولفرام، يعتبر الزمان والمكان شبكات متقطعة من الخلايا (x,t∈N ) يتم تحديثها خطوة بخطوة. ماذا يحدث إذا افترضنا أن العالم فيه كلا النوعين من السلوكيات، المتقطعة والمستمرة؟ سنقدم مثالاً بسيطاً يشير إلى أنه في مثل هذا العالم الحتمية غير كاملة.
نطلق على النماذج التي تحتوي على مزيج من السلوكيات المتقطعة والمستمرة بالنماذج الهجينة. تحتوي النماذج الهجينة على ثقوب (فجوات). لإصلاح هذه الثقوب، علينا إما أن نمنع السلوكيات المتقطعة تماماً، ونؤكد أنها لا تحدث في العالم الفيزيائي، أو علينا أن نتبنّى الفيزياء الرقمية ونضحي بجميع النماذج الفيزيائية المعروفة.
مثال على نموذج هجين، تصادم كرتين كما هو موضح في الشكل (4)، حيث تتحرك الكرة اليسرى نحو الكرة اليمنى بقوة دفع P والكرة اليمنى ثابتة. افترض أن السطح عديم الاحتكاك، وبالتالي يظل زخم momentum كل كرة ثابتاً حتى يحدث التصادم.

يحدث التصادم كحدث منفصل (discrete event) في لحظة ليس لها أي مدة زمنية. فإذا افترضنا أنّ الكراتِ مرنة بشكل مثالي (أي لا يحدث فقْد للطاقة الحركية عند اصطدامها على عكس الواقع الفيزيائي). بالتالي بحسب قوانين نيوتن سيتم الحفاظ على الزخم الكلي والطاقة بعد الاصطدام كما كانت قبله.
بفرض أن الكتلتين متماثلتان، للحفاظ على الزخم والطاقة نحن أمام نتيجتين محتملتين، الأولى: تمر الكرة اليسرى عبر الكرة اليمنى دون التفاعل معها (وهي نتيجة غير مرجّحة). الثانية: تتبادل الكرات الزخم، فتتوقف الكرة اليسرى وتبتعد الكرة اليمنى بنفس سرعة اقتراب الكرة اليمنى قبل الاصطدام (انظر الشكل (4.c)). إذا كان هناك أكثر من كرتين، فإن الموقف يصبح أكثر إثارة للاهتمام.
بفرض أن كرتين تقتربان من كرة ثالثة ثابتة كما هو موضح في الشكل (5.a). فإذا كان للكرات الثلاث نفس الكتلة ماذا سيحدث؟
من المتوقّع في هذه الحالة أن ترتدّ الكرتان الخارجيتان عن الكرة الوسطى وتبتعدان عنها بنفس السرعة التي اقتربتا فيها منها. ليس من السهل الوصول إلى نموذج متقطع (discrete model) قادر على التنبؤ بهذا السلوك.
باعتماد الأسلوب نفسه الذي استخدمناه مع كرتين. إذا كان التصادم متزامناً فإن الكرتين اليسرى واليمنى ستتبادلان الزخم مع الكرة المركزية في الوقت نفسه، وسيكون لهذا الزخم إشارات متعاكسة مما يؤدي إلى إلغاء بعضها البعض. وستتوقف الكرات الثلاث فجأة، وهذا الحل يفشل في الحفاظ على الزخم والطاقة.
الطريقة البديلة -للتعامل مع هذا الموقف- هي التعامل مع التصادمين المتزامنين كلّاً على حدةٍ. كما هو مبيّن في الشكل (5.b) والذي ينتج عنه تباعد الكرات اليمنى واليسرى بسرعات متساوية بعيداً عن الكرة المركزية التي تبقى ثابتة.
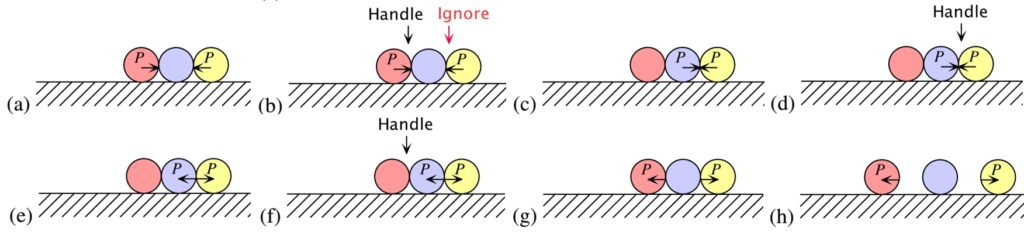
افترض على سبيل المثال، أنّ وزن الكرة المركزية ضعف وزن الكرات اليمنى واليسرى. دعنا نفترض أن الكرة المركزية تزن كيلوغرامين والكرات الخارجية تزن كيلوغراماً واحداً لكل منها. افترض أن الكرتين اليسرى واليمنى تقتربان من الكرة المركزية بسرعة متر واحد في الثانية بحيث تصطدمان في نفس الوقت بالكرة المركزية. الحل الأول: تتبادل الكرتان الزخم وتبقى الكرات الثلاث ثابتة، الحل الثاني: ترتد الكرتان الخارجيتان عن المركز وتتحركان بعيداً عن الكرة المركزية بمعدل متر واحد في الثانية بعد الاصطدام، وكرة المركز تبقى ثابتة. الحل الثالث: نفترض الاصطدام الأيسر يحدث أولاً، وبدون انقضاء أي وقت تحدث الاصطدامات الثانية والثالثة (كما في الشكل (5.b))، أي ستتحرك الكرة اليسرى إلى اليسار بسرعة حوالي 0.48 متراً في الثانية، وستتحرك الكرة الوسطى أيضاً إلى اليسار ولكن بشكل أبطأ حوالي 0.37 متراً في الثانية، وستتحرك الكرة اليمنى إلى اليمين بسرعة حوالي 1.22 متراً في الثانية.
لدينا الآن معضلة حقيقية، وهي ثلاث نتائج محتملة. إذن لا تمنحنا قوانين نيوتن أي أساس لتفضيل أي من هذه الحلول. جميع الحلول الثلاثة وغيرها الكثير متوافقة مع قوانين نيوتن كلهم يحافظون على الزخم والطاقة. نظراً لوجود أكثر من سلوك واحد مسموح به تؤدي قوانين نيوتن (مع الاصطدامات المنفصلة) إلى نموذج غير حتمي. أي أن قبول النموذج الهجين سيفقدنا القدرة على التنبؤ بالا حتمية.
الخاتمة
الحتمية هي خاصية واضحة لا لبس فيها للنماذج ولكنها خاصية غادرة للأنظمة الفيزيائية. جميع النماذج الأساسية في الفيزياء تقريباً حتمية، ويبقى السؤال مفتوحاً حول ما إذا كانت السلوكيات غير الحتمية في جوهرها موجودة في العالم الفيزيائي؟ ونظراً لأن معرفتنا بالعالم الفيزيائي ليست كاملة، فلا يمكننا أبداً التأكيد بشكل قاطع على أن العالم الفيزيائي غير حتمي.
تُظهر الترانزستورات والبوابات المنطقية سلوكاً مخلصاً بشكل غير عادي لنموذج رقمي حتمي. إذ يمكن تشغيل الترانزستورات في الكمبيوتر المحمول وإيقاف تشغيلها مليارات المرات في الثانية والعمل لسنوات دون الانحراف عن السلوك الصحيح الذي يحدده النموذج الحتمي. مثل هذا الإخلاص للنموذج الحتمي لا مثيل له.
يهتم العلم بقدرة النماذج على التنبؤ، بينما تهتم الهندسة بقدرة النماذج على التكرار وتقلل من أهمية التنبؤ، حيث يضمن التكرار أن يتصرف النظام الهندسي كما هو مُصمم وبثقة عالية.
من غير المحتمل أن تقيّد الطبيعة نفسها بمجموعة صغيرة من العمليات الحسابية، ولكن حتى لو لم تكن كذلك، فإن النماذج الحاسوبية للعالم الفيزيائي لا تزال ذات قيمة. نماذج محاكاة الطقس على سبيل المثال، حتمية determinism وفوضوية chaotic ومتقطعة discrete وحسابية computational، ومع ذلك تقوم بعمل رائع في التنبؤ بالطقس لبضعة أيام على الأقل في المستقبل.
= = = = =
*الدكتور المهندس محمد ملحم – أستاذ مساعد في كلية تكنولوجيا المعلومات والاتصالات – جامعة طرطوس.
References
1-Edward Ashford Lee, Plato and the Nerd/ The Creative Partnership of Humans and Technology, MIT Press 2017.
2-https://towardsdatascience.com/the-limits-of-knowledge-b59be67fd50a
3-Earman, J., 1986: A Primer on Determinism, vol. 32 of The University of Ontario Series in Philosophy of Science. D. Reidel Publishing Company, Dordrecht, Holland.
4-Laplace, P.-S., 1901: A Philosophical Essay on Probabilities. John Wiley and Sons, Hoboken, NJ, translated from the sixth French edition by F. W. Truscott and F. L.Emory.
جميع الآراء الواردة في هذه المقالة لا تعبّر بالضرورة عن رأي مركز جي إس إم وإنما تعبّر عن رأي صاحبها حصراً
